The pecking order of a string quartet

Title of paper under discussion

Optimal feedback correction in string quartet synchronization

Authors

Alan M. Wing, Satoshi Endo, Adrian Bradbury and Dirk Vorberg

Date of publication

06 April 2014

Journal

Journal of the Royal Society Interface

Link to original paper (open access)

Overview

This paper investigates the hierarchy of a string quartet. Members of a quartet were monitored during performances to see how well they adjusted their musical pulse to those around them. This revealed leaders and followers within the ensemble.

Experiment

The researchers invited a German string quartet and an English string quartet into their lab (as separate experiments on separate days) and asked them to play an excerpt from the Finale of Haydn’s string quartet op 74 no1:

The instruments were individually mic’ed so that the researchers could take an exact and continuous record of each player’s musical pulse, measured by the time taken between each quaver. A shorter gap between quavers meant a quicker pulse, a longer gap a slower pulse. [In the paper you’ll see that the researchers refer to this gap as the inter-tone interval, or ITI]
As expected the players’ pulses looked pretty stable and uniform throughout the excerpt. But when the researchers zoomed in on the data they could see that players were micro-adjusting their pulse from beat to beat according to what other players were doing in order to stay rhythmically together as an ensemble.
It was this micro-adjustment that was key to revealing the hierarchy – the players who adjusted more were followers, those who adjusted less were leaders.
The research team investigated the adjustment using a technique called time series analysis, a powerful mathematical tool to analyse the effect of ‘X’ on ‘Y’ after a time lag. It’s used by meteorologists, financial traders, epidemiologists – anyone who needs to know how cause and effect may be happening over time.
In our scientists’ investigation, the ‘X’ was musical pulse (or ITI) of one player, the ‘Y’ the musical pulse (or ITI) of a fellow player and the lag was one quaver. That is to say, they wanted to know how the musical pulse (ITI) of a given player at a given moment in the excerpt affected the pulse (ITI) of a fellow player a quaver beat later.
They took the recordings of each player and measured every single ITI in the excerpt. So, for example:

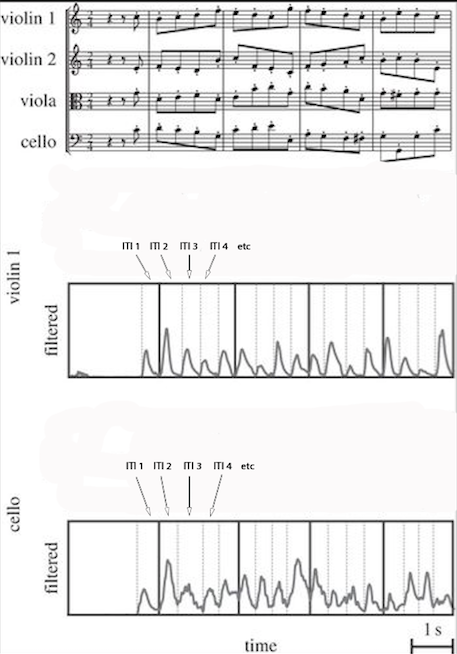
Here the scientists want to know how much the ITIs of violin 1 (‘X’) are affecting the ITIs of cello (‘Y’) a quaver later. So they go through them in turn, seeing how much ITI2 of cello correlates with ITI1 of violin 1; then how much ITI3 of cello correlates with ITI2 of violin 1; then how much ITI4 of cello correlates with ITI3 of violin 1. And so on through the whole excerpt (an experiment that was then repeated fifteen times over to gather as much data as possible), and then again with each paired permutation of players.

Theory
So to recap, by taking the pulse length (or ITI) of each player on each quaver beat, and then looking at the pulse length of another player on the next beat – and so on for every paired combination of players for the whole excerpt – the scientists could build up a detailed picture of which players were adjusting their pulse lengths to which other players. Each player was given a numerical value according to how much they followed or how much they led, a value called alpha (or timing correction coefficient). A high value of alpha meant that a player was very much adjusting their pulse to others; a low alpha meant they were relying on other players to adjust to them.

Dirk Vorberg, the mathematician in the team, showed that the optimal value of alpha for each individual quartet player averages out at 0.25, meaning that for any given difference detected between that player’s ITI and the ITI of a colleague, that player will adjust their next ITI by one quarter of difference. A correction factor greater than 0.25 would mean that players are over-adjusting – any difference in ensemble (eg violin 1 ahead of cello) will be over-corrected and reversed (cello becomes ahead of violin). This over-correction is like when two people approaching one another in a corridor both correct themselves and step one way to avoid each other, then they both step the other way, then back again, so they still can’t pass. A correction factor of less than 0.25 and the players are under-adjusting – so again if the violin 1 is ahead of the cello then neither adjusts enough and so she stays ahead of the cello, just as if our friends in the corridor are approaching one another and neither one of them moves out the way enough.
And crucially, looking at the individual alphas of each the four players in the quartet it is only the average alpha that should be 0.25. It is fine if one player is following much more than leading (so has a higher alpha), so long as his/her colleagues bring down the average by having a lower alpha. 

Results and conclusion

And so it proved in our two quartets – they both exhibited near perfect average values of alpha (0.25). But each quartet made up their average very differently. In the German quartet the leader had a low alpha – she hardly adjusted to her colleagues. But her colleagues made up the difference with relatively high alphas, adjusting to her more than she adjusted to them.

In the English quartet the honours were much more even – each player had an alpha of around 0.25, so the average was equally shared. The authors summarised this as revealing the hierarchy within the quartet, with the German quartet being autocratic and the English one democratic, (a distinction that earned them a nice amount of press coverage in the weeks following publication).
The whole experiment is beautifully summarised in the bar chart below (labelled figure 6 in the paper) where (a) represents the German quartet and (b) the English quartet. The heights of the ‘bars’, variously coloured according to instrument (blue = violin 1, green = violin 2, yellow = viola and brown = cello) correspond to how much they were ‘adjusted to, ‘by the ‘adjusting’ instrument named below.

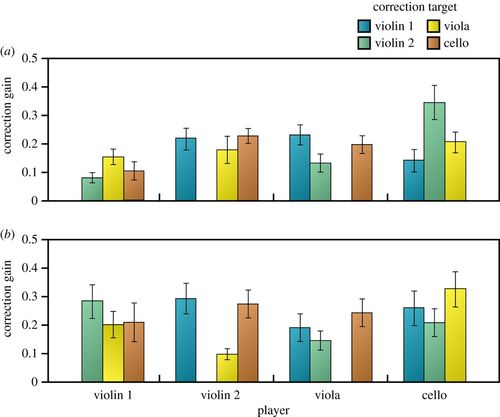
So, for example, looking at quartet (a): violin 1 has three coloured bars above it: green (vn2), yellow (va) and brown (vc) (notice there’s no blue, players are not adjusting to themselves!). But the bar heights are all quite low, especially the green, meaning vn1 is not adjusting much to any of her colleagues, especially not to vn2. But moving along the line, violin 2 is adjusting a good amount to each colleague; as is the viola; as is the cello, whose bar heights are tallest, meaning he is adjusting the most, especially to the vn2 (the very tall green bar).
Quartet (b), the English quartet, have by contrast better matched bar heights from instrument to instrument. There is some variation – violin 2 is not much following viola, whereas cello is very much following viola. But the overall picture is much more democratic.

Thus is revealed the hierarchy of a string quartet, according to who adjusts their timing to whom.

Coda

String Quartet op74 no.1 (finale starts at 14.11) – Joseph Haydn

Amadeus String Quartet