
Title of paper under discussion
Synchronization of complex human networks
Authors
Shir Shahal, Ateret Wurzberg, Inbar Sibony, Hamootal Duadi, Elad Shniderman, Daniel Weymouth, Nir Davidson & Moti Fridman
Journal
NATURE COMMUNICATIONS (2020) 11:3854
Link to paper (free access)
Overview
Eager to investigate how humans synchronise activity in a group, these researchers (led by Shir Shahal from the Faculty of Engineering at Bar-Ilan University, Israel) chose to look at a violin section of 16 players. The violinists, visually and acoustically ‘isolated’ from one another, were asked to play a short phrase over and over again, in unison – as best they could – with other violinist(s) they heard in their noise-cancelling headphones. The scientists had complete control over this headphone feed, manipulating not just which other players each violinist could hear (connectivity) but also how loud were those other players (coupling strength) and how ‘live’ in time they were (delay).
Fascinating strategies emerged in relation to how the violinists coped with trying to synchronise to a delayed feed, including a strong ability to adapt the lengths of their repeated phrase, and to ignore certain ‘frustrating’ players in their headphones. Such strategies add new layers to widely used existing mathematical group synchronisation models (eg the Kuramoto model), and so – according to the authors – promise to influence research into other fields of human interaction eg traffic management, epidemic control and stock market dynamics.

Method and results
Each experiment throughout the whole study involved violinists (on electric violins so their performances were more easily monitored) having to repeat a short musical phrase (see below) over and over for 2 minutes.
The players could not see or hear each other in person, only in their headphones. All players played the first iteration of the phrase with the help of a metronome to ensure everyone was in time and in phase; the metronome dictated that the phrase lasted 4 seconds. The beat then stopped and players were instructed to do their best to synchronise their rhythm with what they heard in their headphones.
Here is a picture of the experimental set-up, plus the phrase they were asked to repeat:

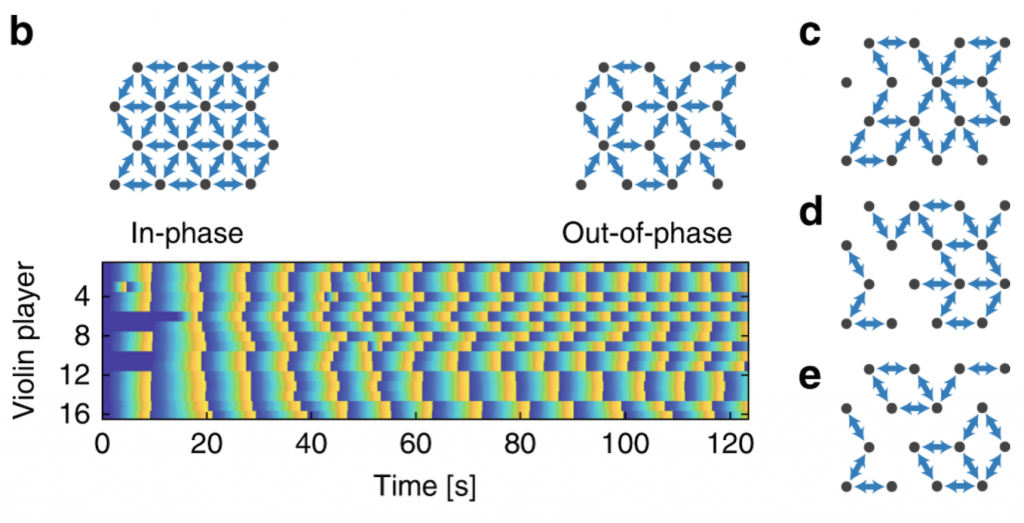
The first experiment saw the scientists unplugging all the headphones such that each violinist could hear only him- or herself. The resultant performances of all 16 players, with the start of each phrase in blue and the end in yellow, look like this on a graph:
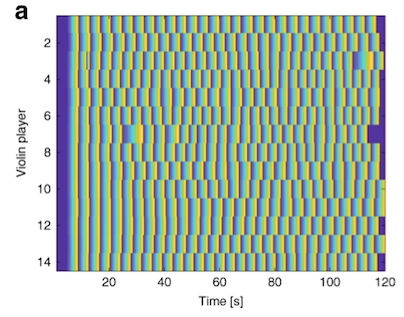
Shahal and her colleagues then set about connecting the headphones, predictably finding that synchronisation was then more successful – although with some ‘connectivity networks’ eliciting better results than others. The network of lowest connectivity, a ‘chain’ in which violinist #16 hears only #15, #15 only hears #14, #14 only hears #13 etc, needed very high ‘coupling strength’ (volume of a violinist’s headphone feed compared to that of their own playing) to achieve good synchronisation. The network of highest connectivity, in which each violinist hears all 15 of his/her colleagues, resulted in excellent synchronisation even with very low coupling strength.
In each of the remaining experiments a delay was introduced into each violinist’s headphone feed. That delay began with a value of 0 secs and gradually increased (linearly) to 4 secs throughout the course of the 2 minute experiment. So, at the beginning of the experiment they heard the other violinist(s) in real time; by half way through the experiment they were hearing them 2 seconds later than real time; and by the end they were hearing them 4 seconds later than real time.
Only two violinists took part in the first of these ‘delay’ experiments. The resulting phrase patterns are presented here:
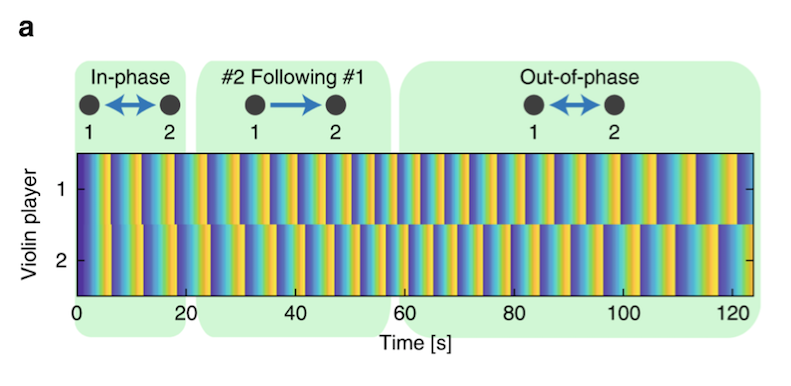
It can be seen that when the delay is zero (beginning of the experiment) the 2 players are able to play ‘in phase’ with one another. As the delay increases, they find it impossible to mutually maintain synchrony, so player #2 starts following player #1 (or rather the delayed broadcast of player #1). Half way through the experiment, which is when the delay reaches 2 secs (being half the length of the 4 second phrase) the players can once again play ‘in synchrony’ to their headphone feed – although an external listener would hear them ‘out of phase’ by half a phrase length, with the 2 second headphone delay it sounds perfectly ‘in phase’ to the players. They then manage to maintain this perfect ‘out of phase synchronisation’ until the end of the experiment, even though the delay keeps on rising, up to an end value of 4 seconds.
The next experiments involved the same design (a gradually increased delay over the course of the 2 minutes), now with an increase in the number of coupled players, though keeping that number even – namely 4, 6 then 8 players. So each player now hears two other players, one in their right ear and one in their left. These groups showed much the same patterns of behaviour as the duo: synchronisation at the start, followed by a period of time during which each player “spontaneously decides to ignore one of its inputs”; then from 60 secs onwards they manage to achieve, and maintain, an ‘out-of-phase synchronisation’.
Of especial interest was the ‘ignoring’ period – the scientists could tell from the data who was ignoring whom. It turned out that there were two patterns of synchronisation depending on who ignored whom: a ‘vortex’, occurring if all players ignore the same side of their headphones and followed the other side, or an ‘arrowhead’, occurring if some players follow one side, and others another side. These patterns are best understood in illustration:
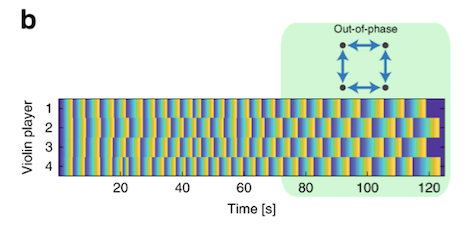
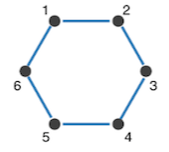
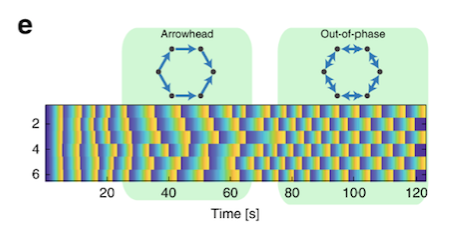
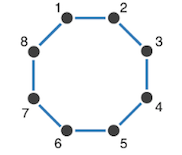
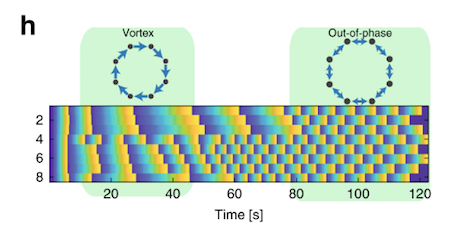
Having investigated an even number of players, Shahal and her colleagues went on to look at an odd number of players. Maths dictates that a closed chain comprising an odd number of players is not going to be able to achieve the stable state of out-of-phase synchronisation that an even number can. [Imagine the phase “hiccup” that can’t be ironed out as final player – #3, #5, or #7 – ‘hands back’ to player #1 in the circle]. In such cases it turns out that “the players spontaneously choose to ignore one of the connections, which breaks the chain and forms an open chain where the out-of-phase synchronisation stage is possible.” This is illustrated here, for 3 then 5 players:
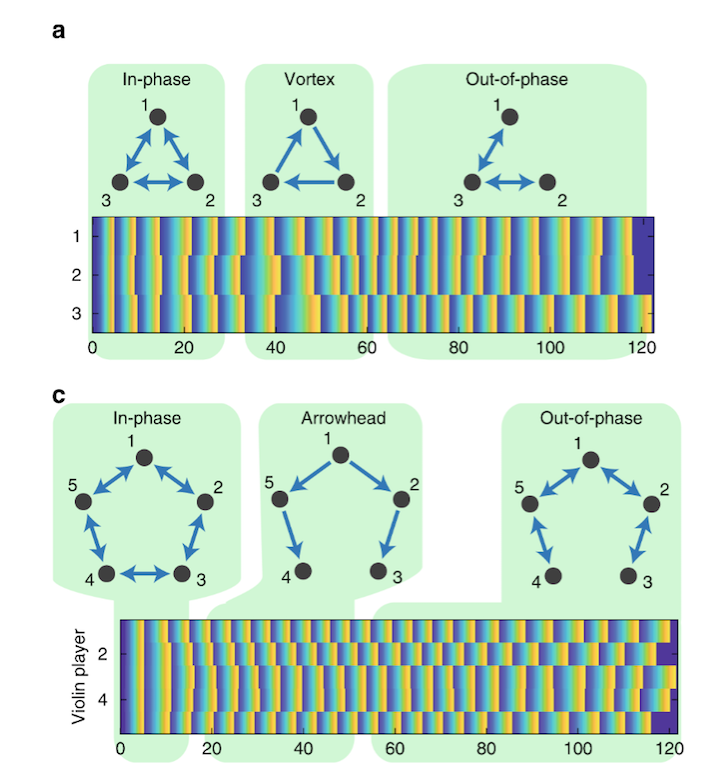
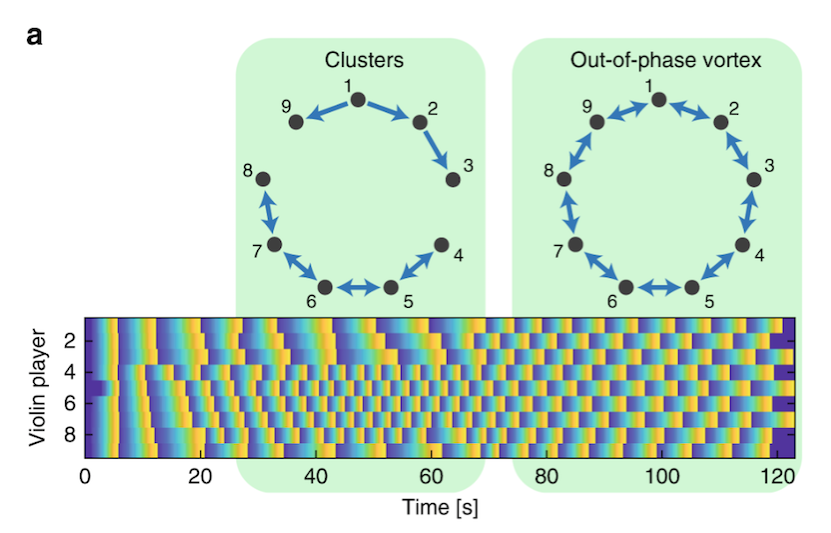
When they reached 9 players, it transpired that the chain didn’t have to break – with that number of players an acceptably small delay could be added by each player in turn which, multiplied by nine, effectively turned them into an even number. Notice how the players divided into two clusters in the first half of the experiment, with one cluster (players #4, #5, #6, #7 and #8) ‘discovering’ a stable out-of-phase synchronisation state before the other (players #9, #1, #2 and #3).
Finally, the researchers increased the connectivity between players by creating ‘lattices’, rather than chains, of communication.
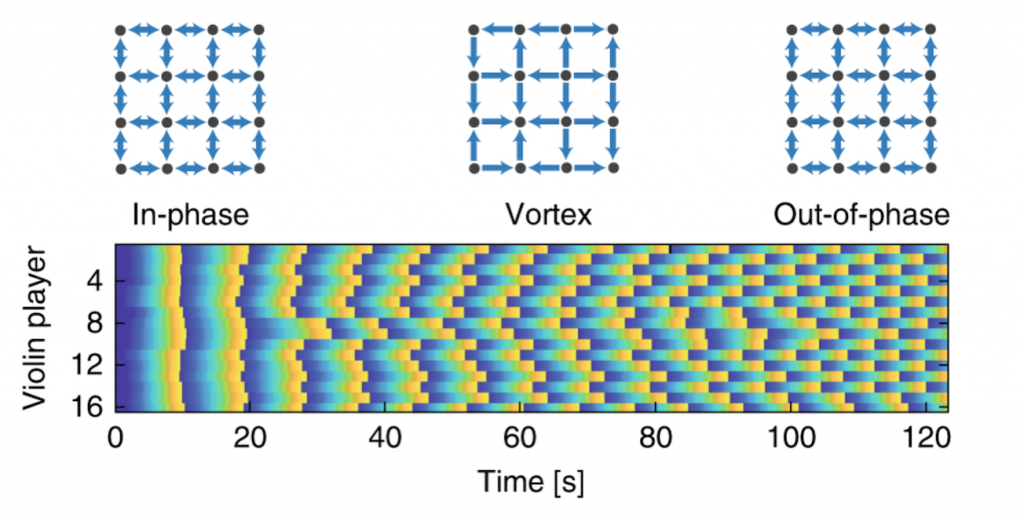
As can be seen below, a square lattice allows players to receive input from up to 4 others:
As the experiment takes its course with a square lattice connection network in place, we see the players’ output evolve from an in-phase synchronised pattern, through a vortex state into a stable state of out-of-phase synchronisation:
The triangular lattice allows players to receive input from up to 6 others:
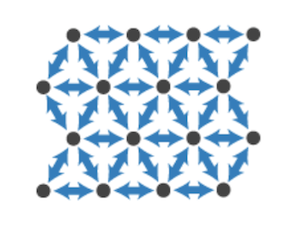
Its experimental output pattern is even more interesting. It starts with in-phase synchronisation but is unable to find a stable out-of-phase synchronisation state – so the players begin to ignore some of the connections, so reducing “the connectivity of the network to one based on square motifs or open chains”. This new connectivity is thus equivalent to a chain with an even number of players, so “can find the highly stable state of out-of-phase synchronisation.” Note from the diagram that on each repetition of this experiment (labelled c, d and e) the players spontaneously discovered different combinations of square motifs and open chains:
Mathematical models
As a finale to their study, our team of scientists played with a mathematical model of network synchronisation – the Kuramoto model – to see how well it might predict the violinists’ behaviour. They discovered that in order to achieve patterns resembling those of the violinists, the model had to be tweaked in two ways:
1) the ‘bandwidth’ of the model’s ‘oscillators’ (analogous to the adaptability of phrase length of the violinists) was too narrow – it had to be able to change by more than the 15% maximum assumed by the current model, reflecting the fact that violinists were able to adapt their phase length by much more than 15% in order to maintain ensemble.
2) the model’s ‘oscillators’ needed to be allowed to ‘delete connections’ to other oscillators, just as our violinists had to ignore other violinists. Present network models aren’t built to delete connections, rather to average them out. Adding such a function helped the models to better mimic the 16 violinists’ behaviour.

Discussion and conclusion
The team discovered that “human networks differ from previously studied networks in the ability of each player to adjust its playing period [phrase length] and to change the network connectivity by ignoring a coupled player and effectively deleting the connection. This ability serves as a unique and efficient mechanism to remover frustrating signals that hinder synchronisation.” They conclude that “the ability of humans to identify conflicts in inputs and to adjust their response accordingly, which is well known, leads to unique dynamics when situated in networks. This research may impact numerous fields, including economics, decision-making research, epidemic spreading, information transfer modelling, traffic control , and more.”
Coda
Piano Phase by Steve Reich
pianos – Art Murphy and Steve Reich